RSA

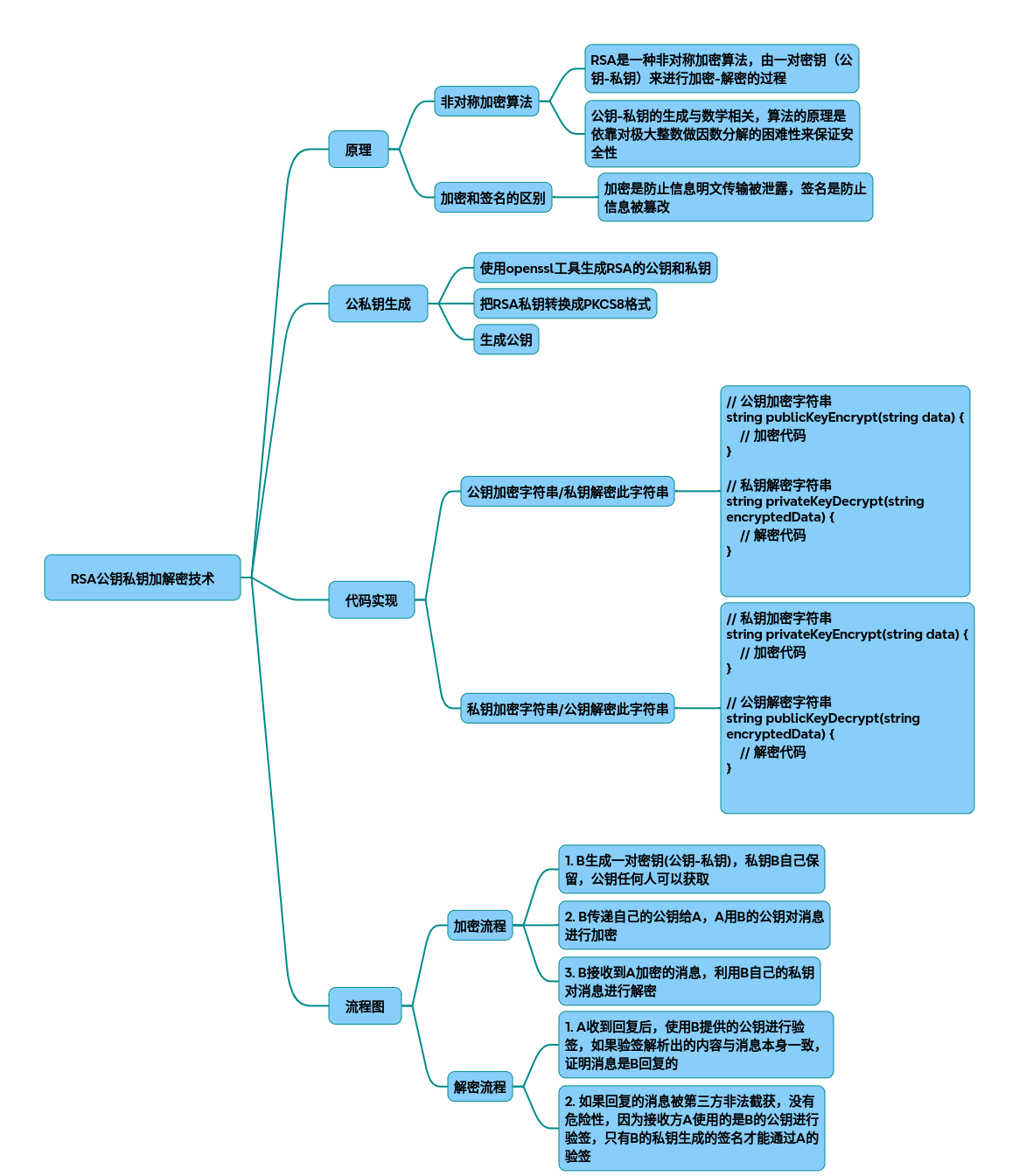
一、RSA技术原理与流程（附流程图）

密钥生成流程

graph TD A[选择大质数p/q] --> B[计算n=p*q] B --> C[计算 “φ（n）=p-1*q-1”] C --> D[选择e与φ（n）互质] D --> E[计算d满足ed≡1 mod φ（n）] E --> F[公钥=e/n, 私钥=d/n]

加解密流程对比

场景	操作方向	数据保护目标	典型应用场景
公钥加密	公钥→私钥	防数据泄露	敏感信息传输
私钥签名	私钥→公钥	防数据篡改	身份认证/数字签名

二、C++完整代码实现（OpenSSL库）

环境配置

# Ubuntu安装OpenSSL开发库
sudo apt-get install libssl-dev

密钥对生成（2048位）

#include <openssl/rsa.h>
#include <openssl/pem.h>

RSA* generate_keypair() {
    RSA *rsa = RSA_new();
    BIGNUM *e = BN_new();
    BN_set_word(e, 65537); // 常用公钥指数 
    RSA_generate_key_ex(rsa, 2048, e, NULL);
    BN_free(e);
    return rsa;
}

公钥加密/私钥解密

std::string rsa_encrypt(RSA* pub_key, const std::string& plaintext) {
    int rsa_len = RSA_size(pub_key);
    std::vector<unsigned char> ciphertext(rsa_len);

    int ret = RSA_public_encrypt(
        plaintext.size(),  
        (const unsigned char*)plaintext.data(), 
        ciphertext.data(), 
        pub_key,
        RSA_PKCS1_OAEP_PADDING // 更安全的填充方式 
    );

    return std::string(ciphertext.begin(),  ciphertext.end()); 
}

std::string rsa_decrypt(RSA* priv_key, const std::string& ciphertext) {
    int rsa_len = RSA_size(priv_key);
    std::vector<unsigned char> plaintext(rsa_len);

    int ret = RSA_private_decrypt(
        ciphertext.size(), 
        (const unsigned char*)ciphertext.data(), 
        plaintext.data(), 
        priv_key,
        RSA_PKCS1_OAEP_PADDING 
    );

    return std::string(plaintext.begin(),  plaintext.end()); 
}

私钥签名/公钥验签

#include <openssl/sha.h>

std::string rsa_sign(RSA* priv_key, const std::string& data) {
    unsigned char hash[SHA256_DIGEST_LENGTH];
    SHA256((const unsigned char*)data.data(),  data.size(),  hash);

    std::vector<unsigned char> sig(RSA_size(priv_key));
    unsigned int sig_len;

    RSA_sign(NID_sha256, hash, SHA256_DIGEST_LENGTH, 
             sig.data(),  &sig_len, priv_key);

    return std::string(sig.begin(),  sig.begin()+sig_len); 
}

bool rsa_verify(RSA* pub_key, const std::string& data, 
               const std::string& signature) {
    unsigned char hash[SHA256_DIGEST_LENGTH];
    SHA256((const unsigned char*)data.data(),  data.size(),  hash);

    return RSA_verify(NID_sha256, hash, SHA256_DIGEST_LENGTH,
                    (const unsigned char*)signature.data(), 
                    signature.size(),  pub_key) == 1;
}

三、关键优化参数与技术

性能优化项

参数类别	可选值	影响维度
密钥长度	1024/2048/4096 bits	安全性与计算开销
填充模式	PKCS1_v1_5/OAEP	抗攻击能力
哈希算法	SHA256/SHA3	签名安全性
大数运算加速	蒙哥马利模乘/CRT优化	解密速度提升40%

典型参数组合示例

// 高性能场景配置 
RSA* rsa = RSA_new();
BN_set_word(e, 65537); 
RSA_generate_key_ex(rsa, 2048, e, NULL); // 2048位密钥 
RSA_blinding_on(rsa, NULL); // 启用盲化抵抗时序攻击 

// 选择OAEP填充增强安全性 
RSA_padding_add_PKCS1_OAEP(ciphertext, rsa_len, plaintext, plaintext_len, NULL, 0);

四、技术扩展建议

密钥存储方案：使用PKCS#8标准存储私钥（PEM格式加密）
混合加密体系：RSA传输AES密钥（结合对称加密）
抗量子计算：探索NTRU/Lattice-based后量子算法
硬件加速：通过OpenSSL ENGINE接口调用HSM加速卡

完整代码示例与性能测试数据可参考。如需更深入的数学证明或特定语言移植方案，可进一步提供需求细节。

完整代码

Github